
Johannes Kepler, 1571-1630.

Johannes Kepler est un astronome allemand à qui nous devons beaucoup : Il a élucidé les mystères des orbites des planètes autour du Soleil, et en a sorti 3 lois qui sont aujourd'hui les fondements de la mécanique céleste. Grâce à lui, nous pouvons estimer avec une grande précision la distance, la taille, la vitesse des objets qui parcourent le système solaire. Il croyait également que les 6 planètes connues à l'époque étaient imbriquées dans les 5 solides parfaits de Platon, qu'on appelle polyèdres, et que la perfection de cette horloge était la preuve du génie de Dieu, notre créateur.
Scolarité et études du jeune Kepler
Astronome et physicien allemand, Johannes Kepler est né le 27 Décembre 1571 à Weil der Stadt, dans le Wurtemberg. (Sud-ouest de l’Allemagne).
Kepler vit chez ses grands-parents de 1574 à 1576, il part ensuite avec ses parents à Léonberg où il entre à l’école latine. A trois ans, il attrape la petite vérole, il s’en sort avec les mains déformées, des yeux affaiblis et une santé précaire. Il garde néanmoins une intelligence au dessus de la normale.

Initié à l'héliocentrisme en cachette
En 1584, il entre au séminaire protestant d’Adelberg , mais il est repéré en 1587 par le duc de Wurtemberg qui décide de le prendre sous sa tutelle. Il fréquente alors l’université de Tübingen où il suit les cours de Michael Maestlin, son professeur de mathématiques (qui fut l’un des premiers à adhérer au système héliocentrique de Copernic). Maestlin se contentait pourtant de donner des cours sur le système géocentrique de Ptolémée, mais il donnait en secret des précisions aux élèves les plus doués (comme Kepler) sur l’héliocentrisme. A l’université, Kepler lit beaucoup et s’intéresse fortement à la théologie, il est également initié à l’astrologie et à la philosophie de la nature d’Aristote, à laquelle il restera longtemps attaché. Il dira qu’il adhéra à la théorie de Copernic grâce à Maestlin, pour des raisons métaphysiques.
Il passe son examen de fin d’études en 1591 et poursuit en tant qu’étudiant diplômé. Il ambitionne alors de devenir ministre luthérien. Pourtant, après la mort du professeur de mathématiques du séminaire protestant de Gratz, Tübingen recommande Kepler pour prendre le poste vacant. Il accepte, à contre cœur. Pendant six années, il y enseignera la géométrie, l’arithmétique, Virgil et la rhétorique.

Sa vision de l'Univers
Les solides de Platon appliqués au système solaire
En 1595, en traçant un triangle dans un cercle, il a une idée qu’il juge extraordinaire : « Il y a six planètes parce qu’il y a cinq solides parfaits, un solide parfait s’intercalant exactement entre deux planètes ». Kepler croyait que le nombre et la disposition des planètes était une manifestation de la volonté de Dieu et non le fruit du hasard. Il encastre alors les 6 planètes connues à l'époque dans les 5 solides parfaits platoniciens. A chaque sphère est associée une planète, le rayon de la sphère donne la distance moyenne de la planète au Soleil. Chaque polyèdre est inscrit dans une sphère et circonscrit dans une autre.
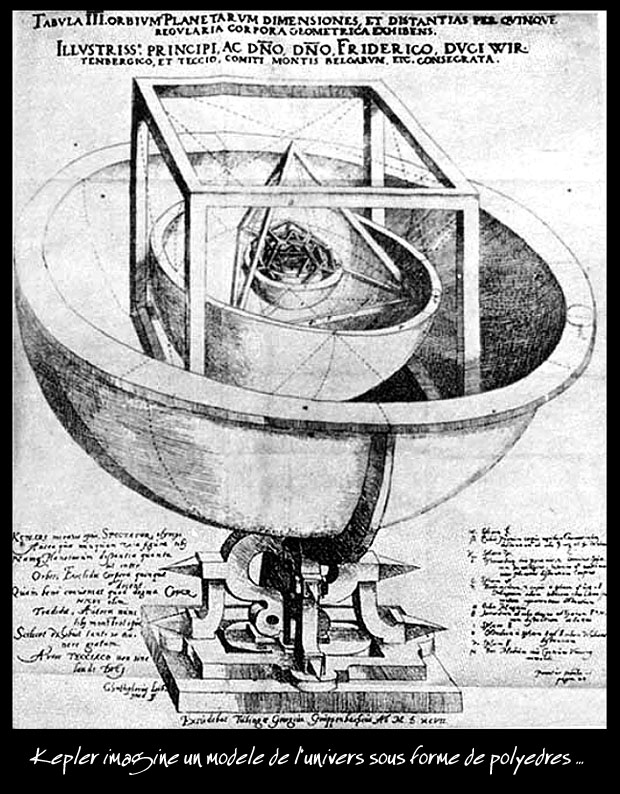
Selon Kepler, Vénus correspond à l'octaèdre, la Terre à l'icosaèdre, Mars au Dodécaèdre, Jupiter au tétraèdre et Saturne au cube. Il pense donc que les distances entre les planètes et le Soleil dans le système héliocentrique sont déterminées en fonction des cinq solides réguliers (établis par Platon), si on suppose que l’orbite d’une planète est circonscrite à un solide et déterminée par un autre solide (il croit encore, à l’époque, que les orbites sont circulaires).
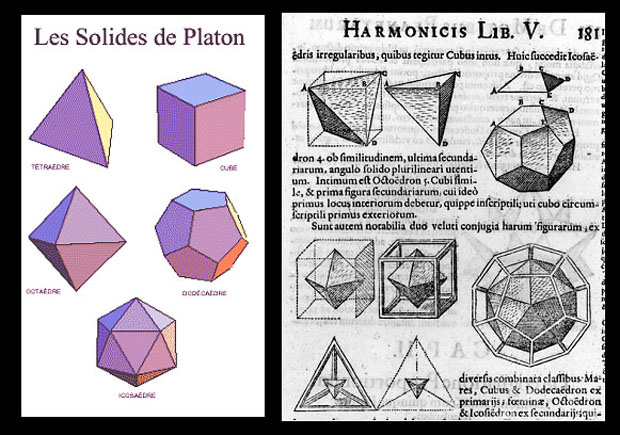
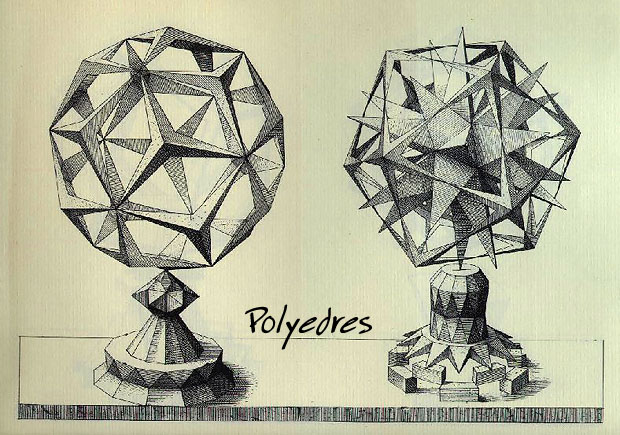

Le tétraèdre
Il est composé de 4 faces qui sont des triangles équilatéraux. Il a 4 sommets et 6 arêtes. Il a 3 arêtes en chacun des sommets. Chez les grecs, il était le symbole du feu.
Le cube
Il est composé de 6 faces qui sont des carrés. Il a 8 sommets et 12 arêtes. Il a 3 arêtes en chacun des sommets. Chez les grecs, il était le symbole de la Terre.
L'octaèdre
Il est composé de 8 faces qui sont des triangles équilatéraux. Il a 6 sommets et 12 arêtes. Il a 4 arêtes en chacun des sommets. Chez les grecs, il était le symbole de l'air.
Le dodécaèdre
Il est composé de 12 faces qui sont des pentagones réguliers. Il a 20 sommets et 30 arêtes. Il a 3 arêtes en chacun des sommets. Chez les grecs, il était le symbole de l'univers.
L'icosaèdre
Il est composé de 20 faces qui sont des triangles équilatéraux. Il a 12 sommets et 30 arêtes. Il a 5 arêtes en chacun des sommets. Chez les grecs, il était le symbole de l'eau.
Collaboration avec Tycho Brahé
Il entame alors des travaux qu’il approfondit à l’aide de calculs et les publie en 1596 sous le titre de Mysterium Cosmographicum. A l’exception de Mercure, les travaux de Kepler produisent des résultats étonnants. Il envoie une copie de son œuvre à Tycho Brahé, alors mathématicien impérial. Ce dernier est impressionné par le talent du jeune Kepler et l’invite à venir l’assister à Prague pour calculer les nouvelles orbites des planètes (notamment Mars qui présentait des anomalies incompréhensibles, comme le mouvement rétrograde) pour ses observations. Johannes Kepler part de Gratz en 1600.
Le mystère de l'orbite de Mars
Kepler se base alors sur les formidables données observationnelles de Tycho Brahé sur la planète Mars, et se rend vite compte qu'il ne peut appliquer pour cette planète une orbite circulaire ... Pourtant, après de nombreux calculs établis à partir de 4 positions de Mars sur son orbite, il arrive à déterminer une orbite circulaire avec le Soleil comme point équant (point symétrique avec le cercle orbitale). Il faut dire que cette conclusion est le résultat de multiples erreurs de calculs qui se sont additionnées, compensées et annulées, et si ce résultat le conforte avec sa théorie des orbites circulaires, deux nouvelles observations mettent à plat tout son travail ! Il découvre un écart de plus de 8' avec la théorie ... Théorie à laquelle il décide immédiatement de renoncer.
Brahé meurt en 1601 et Kepler lui succède alors en tant que mathématicien impérial, le poste le plus prestigieux en Europe. En 1604, il publie Astronomia pars Optica, dans lequel il expose une théorie sur la réfraction atmosphérique, il traite également de l’optique en donnant une explication moderne sur le fonctionnement de l’œil.
2 ans plus tard, il publie De Stella Nova, au sujet d’une nouvelle étoile apparut dans le ciel en 1604.
..jpg)
Les 2 premières lois de la mécanique céleste
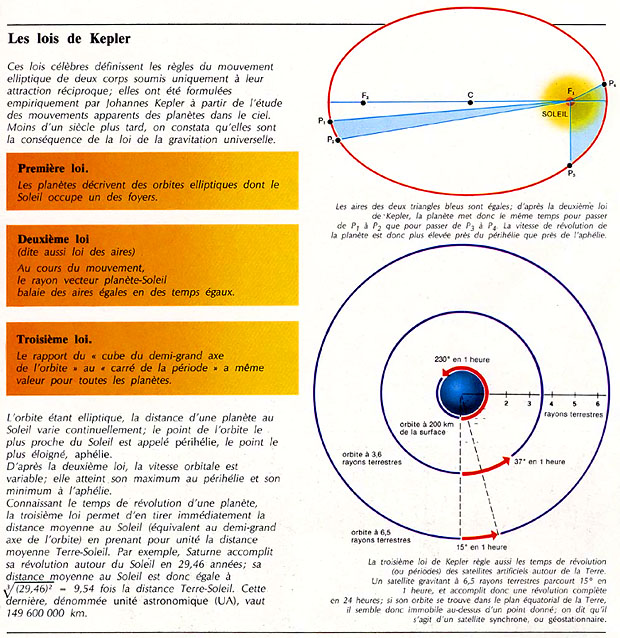
En 1609, il sort Astronomia Nova, contenant deux de ses nouvelles lois du mouvement planétaire, appelées « lois de Kepler ». La première, stipule que les planètes se meuvent autour du Soleil selon des orbites elliptiques, la seconde (règle des aires) dit que la ligne imaginaire que l’on tracerait entre le Soleil et une planète balaie des aires identiques d’une ellipse pendant des intervalles de temps égaux. Pour simplifier, plus la planète se rapproche du Soleil, plus sa vitesse est importante.
En fait, Kepler découvre la deuxième loi avant la première. Il découvre la loi des aires en rééxaminant en détails l'orbite de la Terre, car c'est pour lui la première chose à faire pour comprendre l'orbite de Mars, et se rend compte que la durée que met la Terre à parcourir une certaine distance est proporitionnelle à son éloignement du Soleil. Et c'est à l'aide de cette loi des aires qu'il arrive à visualiser l'orbite de Mars, en combinaisant de nombreux positions : Une ellipse, dans laquelle le Soleil occupe l'un des foyers.
A cette époque, les autres astronomes s’obstinent à suivre le vieux précepte selon lequel l’étude des planètes est un problème de cinématique, Kepler pencha pour une optique plus dynamique, il introduit la physique en astronomie. Surtout, en travailleur acharné et intègre qu'il est, il s'inflige une discipline de fer en exigeant à ses théories une validation absolue par l'observation, quitte à y renoncer s'il n'est pas convaincu : En ce sens, il devient un scientifique moderne.
Un soutien de poids pour Galilée
En 1610, Galilée découvre, à l’aide du télescope qu’il vient d’inventer, les quatre satellites de Jupiter (Io, Europe, Ganymède et Callisto). Johannes Kepler, envoie une lettre de soutient à l’astronome italien qu’il publie sous le titre de Dissertio cum Nuncio Sidero (conversation avec le messager des étoiles). L’année suivante, il obtient l’autorisation d’observer les quatre satellites de Jupiter à la lunette astronomique et publie ses observations dans un ouvrage intitulé Narratio de Observatis Quator Jovis Satellibus (récit des quatre satellites de Jupiter observés). Cette publication fut alors un appui de poids pour Galilée qui avait du mal à faire admettre ses observations, danc un contexte d'obscurantisme religieux.
La vie mouvementée de Kepler
Humainement, Kepler a de gros problèmes personnels malgré le succès. Il est souvent à cours d’argent car il a de nombreux créanciers qui le harcèlent, et on lui paie mal ses honoraires … Il doit également fréquemment fuir, car il est souvent la cible de l’inquisition qui traquent sans relâche les hérétiques à cette époque. Sa vie familiale n’est pas non plus une réussite, la première de ses deux épouses meurt brutalement en 1610 à Prague, et il voit également deux de ses enfants mourir.
La 3ème loi de mécanique céleste
En 1612, Kepler est nommé mathématicien des Etats de la Haute-Autriche. Il publie sept ans plus tard Harmonices Mundi. Dans cet ouvrage, il expose sa troisième loi. Le cube de la distance entre une planète et le Soleil divisé par la période orbitale de cette planète au carré est une constante et est la même pour toutes les planètes. Dans la foulée, il publie un recueil de toutes ses découvertes : Epitome Stronomiae Copernicanae (Abrégé d’astronomie copernicienne), qui devient la plus influente introduction à l’astronomie de type copernicien.
Un scientifique toujours imprégné de sa religion
Parallèlement à ses recherches astronomiques, Kepler s’intéresse toujours à la théologie et il publie, en 1613, un ouvrage sur la chronologie et la naissance du Christ (De Vero Anno quo Aetermus Dei Filius Humanam in Utero Benedictae Virginis Mariae Assumpsit) dans lequel il démontre que le calendrier chrétien est erroné de cinq ans et que Jésus Christ serait en fait né en -4 av J.C ... Conclusion désormais acceptée.
En 1618 débute la Guerre de Trente ans, qui envahi la plupart des régions allemandes et autrichiennes. Les opposants à la Réforme commencent à persécuter les protestants en Autriche : Kepler en fait partie (il réside à Linz, capitale de cette province), mais il n’est pas inquiété du décret qui bannit tous les protestants de cette province, du fait de son statut officiel.
La dernière œuvre majeure de Kepler est Tabulae Rudolfinae (Tables rudolfines), en 1625, œuvre contenant les nouvelles tables basées sur les observations de Tycho Brahé et calculées en partenariat avec l’astronomie de Kepler. Isaac Newton s’inspira fortement des théories et des observations de Kepler pour formuler sa théorie sur l’attraction universelle.
En raison de la guerre, l’imprimerie qui éditait ses œuvres fut détruite et on a perdu toute trace de son monument. Ses manuscrits ont été sauvés par Catherine de Russie, ils se trouvent désormais à l’Observatoire de Polkovo, à Saint-Pétersbourg.
Johannes Kepler meurt en 1630, à l’âge de 59 ans.

Notre sélection de videos sur l'astronomie :
Un commentaire ? Laissez-donc vos impressions !





